Auf Social Media ist es ein beliebter Sport: Man gibt einem modernen Sprachmodell eine einfache Rechenaufgabe - und freut sich, wenn es patzt. Schon hat man scheinbar den Beweis, dass diese Systeme gar nicht intelligent sein können. Das Argument ist eingängig, unterhaltsam, und in einer Debatte, in der manche ernsthaft von naher AGI sprechen, wirkt es wie ein notwendiger Realitätscheck. Doch dieser Schluss führt in die Irre. Arithmetik ist ausgerechnet die Disziplin, in der heutige Sprachmodelle architektonisch benachteiligt sind – und das sagt weit weniger über ihre tatsächliche Fähigkeit zu folgerichtigen Schlüssen aus, als oft behauptet wird. Und wenn man versteht, wie sie arbeiten, offenbart ihr Verhalten bei arithmetischen Aufgaben sogar ein bemerkenswertes Abstraktionsvermögen.
Die Forschung zeigt ein konsistentes Muster von Schwächen:
- Modelle verallgemeinern schlecht auf längere Zahlen. Wer Addition mit 3-stelligen Zahlen lernt, scheitert oft an 4-stelligen - die Antworten liegen zwar oft im richtigen Bereich, aber sind z. B. um eine Ziffer falsch. [Lee 24]
- Multiplikation besonders anfällig. Selbst leistungsstarke Modelle wie GPT-4 machen häufig Fehler bei einfachen Mal- und Geteilt-Aufgaben. [Li 24]
- Ungefähre Antworten statt klarer Regeln. Analysen zeigen: Sprachmodelle schätzen Summen über Fourier-ähnliche Merkmale und Heuristiken. [Zhou 24]
- Architekturbedingte Grenzen bei Zählaufgaben: Bei binären Sequenzen wie 111011101... scheitern Modelle ab einer bestimmten Länge zuverlässig an der exakten Zählung der Einsen [Barbero 24]

Sprachmodelle sind Zahlenblind
Sprachmodelle sind darauf trainiert, Konversationen zu vervollständigen. Sie sind für Sprache optimiert, nicht für Zahlen. Und schon in der Darstellung von Zahlen hat das System eine Schwäche: Tokenisierung. Anstatt Worte (und Ziffernketten) als unteilbare Einheiten zu sehen, zerlegt ein moderner Tokenizer Text in Subwörter - eine brillante Idee für natürliche Sprache, weil sie das Vokabular effizient hält und Out-of-Vocabulary-Fehler vermeidet. Für Zahlen ist das aber tückisch Die Aufgabe „1101 + 10010 = 11111“ zerfällt (mit einem LLaMA 3 Tokenizer) zu "110","1","+","100","10","=","111","11".
Ähnliche Tokens wie “10” und “11” werden im Vokabular des Tokenizers zu Tokens, die nichts miteinander zu tun haben (IDs “605” und “806”). Bedeutung entsteht erst aus Mustern im Training. Ziffern sieht das Sprachmodell nicht. Tokens kennen keine Stellenwerte. Das Subtoken „110“ steht in „1101“ für Tausender-Hunderter-Zehner, in „10010“ dagegen für Zehntausender-Tausender-Hunderter. Tokens wissen nichts von Stellenwerten; sie sind bloße Textbausteine. Aus so einer Darstellung ein robustes Rechensystem zu lernen, ist denkbar schwierig: Das Modell muss Mappings zwischen Tokenmustern internalisieren. Auch wenn LLMs regelmäßig Rechenfehler machen, liegen die Ergebnisse selbst im Fehlerfall oft erstaunlich nah am Sollwert - ein Hinweis darauf, dass die Modelle effektive Heuristiken erlernen.
Attention Defizit - Numerische Grenzen der Transformer
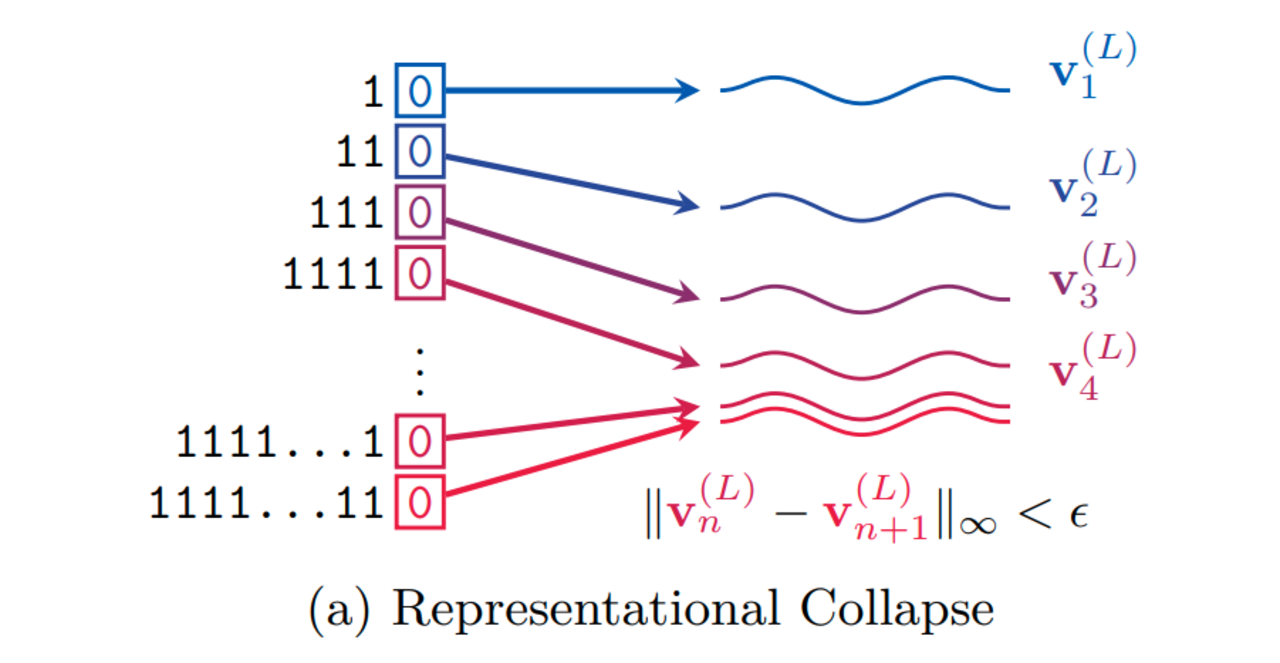
Die Tokenisierung ist nicht die einzige Hürde. Auch der Attention-Mechanismus, das Herzstück moderner Transformer, zeigt Schwächen, sobald es um arithmetische Operationen geht. Ein besonders anschauliches Beispiel liefert das Paper "Transformers Need Glasses"(Barbero et al., 2024). Darin untersuchten die Autoren, wie Sprachmodelle einfache Zählaufgaben bewältigen - etwa das Bestimmen der Anzahl von Einsen in einer binären Sequenz wie 111010001...
Das Ergebnis: Transformer stoßen auf eine fundamentale Grenze. Weil Attention Eingaben durch eine Folge von Matrixmultiplikationen in kontinuierliche Repräsentationen verdichtet, kommt es bei hinreichend langen Sequenzen zu Informations-Kollisionen. Ab einem gewissen Punkt unterscheiden sich die internen Vektoren so wenig, dass zwei verschiedene Eingaben - etwa eine Sequenz mit 99 Einsen und eine mit 100 Einsen - im Modell praktisch ununterscheidbar werden. Die Architektur selbst zwingt also bestimmte Fehler herbei.
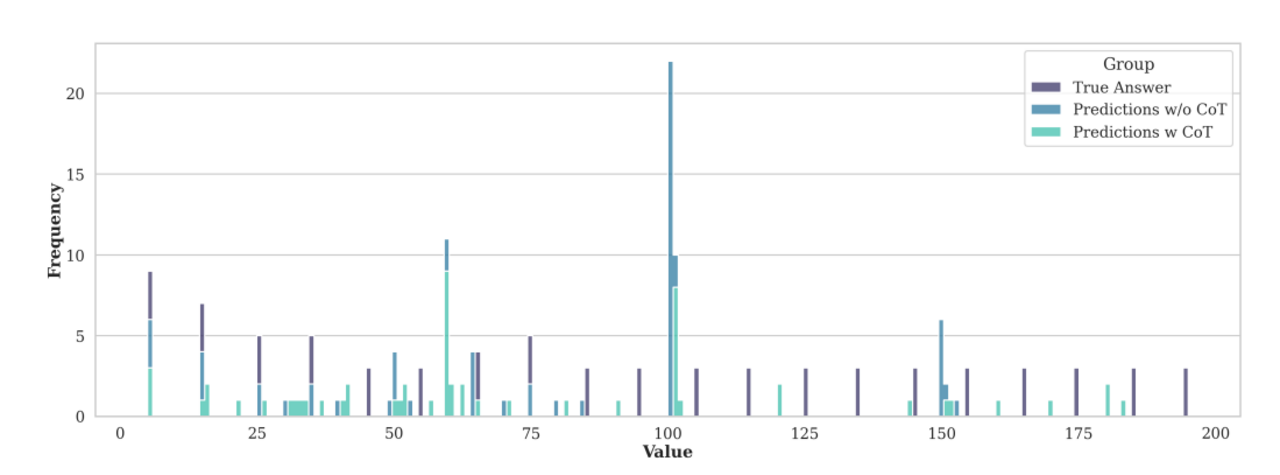
In Experimenten zeigte sich, dass Modelle schon weit vor diesem theoretischen Limit versagen. Sie entwickeln dabei charakteristische Fehlermuster: Bestimmte Antworten tauchen überproportional häufig auf, etwa die Schätzung, dass eine lange Sequenz „100 Einsen“ enthält - unabhängig davon, wie viele es tatsächlich sind.
Die Forschenden deuten dieses Verhalten als eine Art Subitizing- jenes psychologische Phänomen, bei dem Menschen kleine Mengen von Objekten spontan und ohne Zählen erkennen können, während größere Mengen nur noch ungefähr eingeschätzt werden. Sprachmodelle scheinen etwas Ähnliches zu tun: Anstatt algorithmisch exakt zu zählen, intuieren sieMengen bis zu einer gewissen Größe und scheitern, sobald die Eingabe anspruchsvoller wird.
Bessere Zahlendarstellungen – Kosmetische Lösungen für fundamentale Grenzen
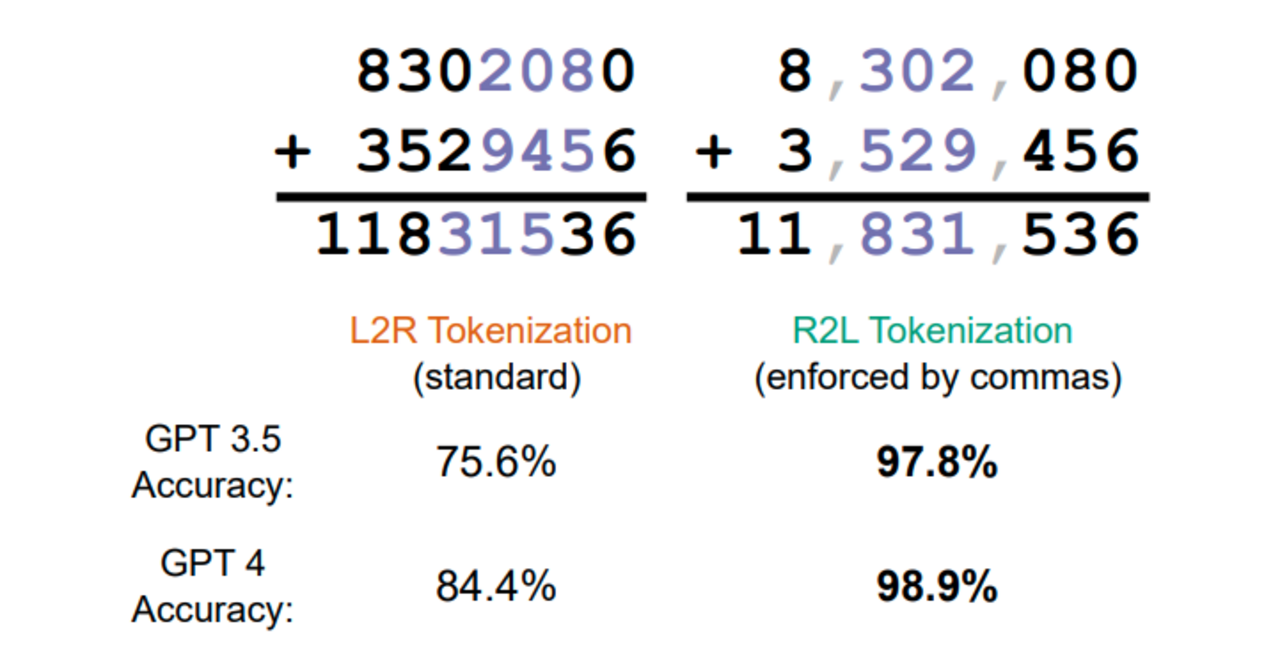
Forschungsarbeiten zeigen, dass sich Arithmetik durch spezialisierte Zahlendarstellungen verbessern lässt. So erleichtert eine rechts-nach-links-Tokenisierung Überträge (Singh & Strouse 24), während Abacus Embeddings jeder Ziffer zusätzlich ihre Stellenposition mitgeben und damit auch lange Additionen ermöglichen (McLeish 24). Andere Ansätze nutzen explizite Stellenwertkodierungen(Nogueira 21) oder strukturierte Symmetrien(Sabbaghi 24).
Doch all diese Methoden haben einen Preis: Spezialisierung ist immer ein Trade-off. Ein Tokenizer, der Ziffern perfekt repräsentiert, ist für Sprache weniger effizient; zusätzliche numerische Module erhöhen Komplexität und Speicherbedarf. Und das grundlegende Problem des Attention-Mechanismus, dass exaktes Zählen über lange Sequenzen architekturbedingt instabil wird, bleibt davon unberührt.
Gleichzeitig verfügen moderne Modelle bereits über eine andere Art, mit Problemen dieser Art umzugehen: Sie greifen auf Werkzeuge zurück. GPT-4, Claude oder Gemini können Python-Code generieren, eingebaute Rechenmodule ansteuern oder API-Tools nutzen, um exakte Ergebnisse zu berechnen und diese in ihre Schlussfolgerungen einzubetten. Sie lösen damit mathematische Aufgaben so, wie es auch Menschen tun: indem sie Werkzeuge zur Hilfe nehmen.
Arithmetische Fehler sind kein Beweis gegen Reasoning. Sie sind ein Artefakt von Repräsentation und Architektur. Sprachmodelle sehen nicht, wie Ziffern sich zu Zahlen zusammensetzen oder wie man sie zuverlässig algorithmisch verarbeitet. Trotzdem entwickeln sie nützliche Heuristiken und nutzen Werkzeuge, um Aufgaben zu lösen. Es wirkt daher ironisch, wenn die Schwäche bei Kopfrechnen als Beleg gegen die Intelligenz dieser Systeme angeführt wird, wo sie doch vor allem ihre Parallelen zu menschlichem Denken offenbaren. Denn auch Menschen haben Schwierigkeiten, vierstellige Multiplikationen im Kopf zu bewältigen – und greifen zu Hilfsmitteln.
Datum: 19.08.2025
Bildquelle: KI-generiert
In unserer monatlichen Serie “KI-Journal Club” stellen wir wissenschaftliche Beiträge und Presseberichte vor aus den Bereichen Text Mining, Machine Learning, Generative Künstlicher Intelligenz & Natural Language Processing.
Wir beraten Sie gerne.
Sprechen Sie uns an

Bertram Sändig
Bertram ist Experte für KI- und Machine-Learning-Systeme mit einem Fokus auf NLP und Neural Search. Er hält einen B.Sc. in Informatik der FH Brandenburg und seit 2018 einen M.Sc. der TU Berlin mti den Schwerpunkten Machine Learning und Robotik. Parallel zum Studium war er fünf Jahre Leitender Software-Ingenieur im Space Rover Project des Luft- und Raumfahrtsinstituts der TU-Berlin. 2018 stieg er als Machine Learning Engineer bei Neofonie ein und leitet heute das Machine Learning Team bei ontolux, einer Marke der Neofonie GmbH. Mit großer Leidenschaft überführt er aktuelle Forschungsergebnisse in nutzbare Anwendungen für Kunden, vor allem an der Anpassung, Optimierung und Integration von Large Language Modellen in Suchsysteme und das Textanalyse-Toolkit von ontolux.
