Vektoreinbettungen (Embeddings) gelten als das fundamentale Rückgrat moderner KI-Suchsysteme. Doch aktuelle Forschung zeigt: Es gibt harte theoretische Grenzen. Wir analysieren, warum Vektoren an simplen Aufgaben scheitern und was JPEG-Bilder damit zu tun haben.
In der aktuellen Landschaft der Künstlichen Intelligenz ist das Paradigma fast immer dasselbe: Ob in RAG-Pipelines (Retrieval-Augmented Generation) oder semantischen Suchmaschinen – wir transformieren komplexe Dokumente in dichte Vektoren fixierter Länge (Embeddings). Die Hoffnung dabei: Die semantische Essenz des Textes wird in diesem geometrischen Raum konserviert.
Das Prinzip der semantischen Geometrie besagt, dass ähnliche Konzepte (wie Hund und Wolf oder Äpfel und Bananen) räumlich nahe beieinanderliegen. Die Bedeutung entsteht durch die relative Position der Punkte zueinander.
Ein bemerkenswertes aktuelles Paper mit dem Titel "On the Theoretical Limitations of Embedding-Based Retrieval" (Weller et al., 2025) stellt diese Annahme jedoch radikal infrage. Die Autoren zeigen, dass das Scheitern bei bestimmten Aufgabenstellungen nicht an mangelndem Training liegt, sondern eine harte, mathematische Unmöglichkeit darstellt.

Das LIMIT-Datenset: Täuschende Einfachheit
Um diese These zu beweisen, konstruierten die Autoren den Datensatz LIMIT (Linguistically Simple, Geometrically Impossible Task). Auf den ersten Blick wirken die Dokumente trivial: Es handelt sich um synthetisch generierte, kurze Listen von Attributen, die fiktiven Personen zugeordnet sind. Linguistisch gibt es hier weder komplexe Syntax noch Mehrdeutigkeit.
Betrachten wir zwei Beispiele aus dem Datensatz:
doc1 "Olinda Posso":
- Olinda Posso likes Bagels, Hot Chocolate, Pumpkin Seeds, The Industrial Revolution, Cola Soda, Quinoa, Alfajores, Rats, Eggplants, The Gilded Age, Pavements Ants, Cribbage, Florists, Butchers, Eggnog, Armadillos, Scuba Diving, Bammy, the Texas Rangers, Grey Parrots, Urban Exploration, Wallets, Rainbows, Juggling, Green Peppercorns, Dryers, Pulled Pork
doc2 "Wynona Meskell":
- Wynona Meskell likes Pad Thai, Egg Noodles, Woodpeckers, Adventure Video Games, Chili, the Chicago Cubs, Love, Duct Tape, Upside-Down Cakes, Leaf Blowers, Apple Cider, Video game music, The Progressive Era, Fossils, Sugar Gliders, Yeast, Bath Mats, Komodo Dragons, the San Diego Padres, White Rice
Die Aufgabenstellung für das Retrieval-System ist simpel: "Finde alle Personen, die X mögen".
Während klassische, Keyword-basierte Verfahren wie BM25 (Sparse Retrieval) diesen Task mühelos lösen, brechen moderne Dense Retrieval Modelle (wie SOTA-BERT-basierte Bi-Encoder) hier dramatisch ein. Ihre Genauigkeit sinkt auf ein Niveau, das die Nützlichkeit des Systems infrage stellt.
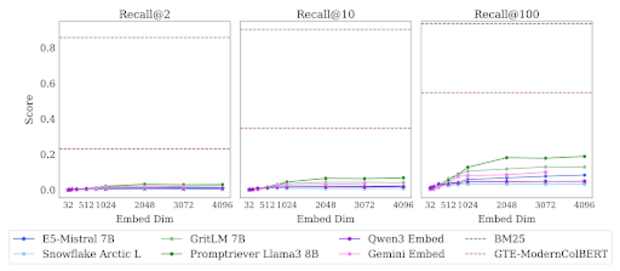
Der Realitäts-Check: Ein Desaster für Dense Retrieval
Ein Blick auf die Leistungsdaten aktueller Spitzenmodelle bestätigt die Theorie eindrucksvoll. Wie die folgende Grafik verdeutlicht, scheitern moderne Dense-Retrieval-Ansätze an dieser Aufgabe fast vollständig.
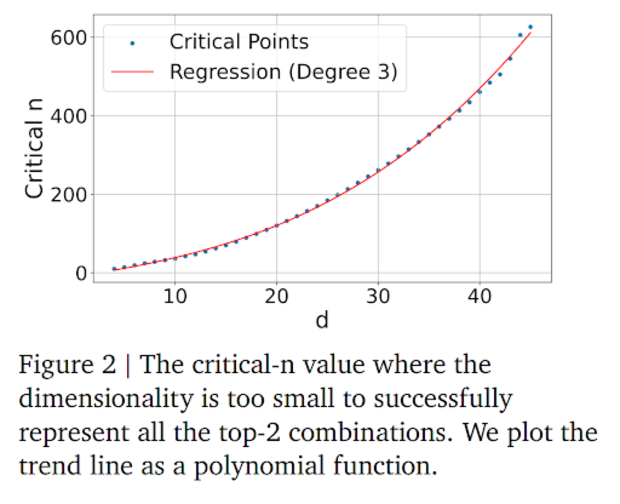
Der empirische Beweis: Optimierung jenseits des Lernens
Das wohl faszinierendste Experiment des Papers schließt aus, dass es sich hierbei um ein Versagen des "Lernens" handelt. Die Autoren umgingen den Encoder (das neuronale Netz) vollständig. Anstatt zu versuchen, ein Modell zu trainieren, das Texte auf Vektoren abbildet, nutzten sie direkten Gradient Descent, um die Vektoren selbst auf dem Test-Set zu optimieren.
In der Praxis des Machine Learning würde man dies als "Data Leakage" oder schlichtes Schummeln bezeichnen. Es ist der theoretische Best Case: Wir fragen nicht, was das Modell lernen kann, sondern ob es überhaupt eine geometrische Anordnung von Vektoren im Raum gibt, die diese Retrieval-Aufgabe lösen könnte.
Punkte oberhalb der roten Linie sind geometrisch unmöglich – egal wie lange man trainiert. Da reale Modelle (wie BERT oder Ada-002) generalisieren müssen, liegt ihre Performance weit unterhalb dieser idealisierten Kurve. Wenn selbst die theoretisch perfekte Optimierung scheitert, haben reale Modelle bei fixer Dimension keine Chance, die komplexen Relevanz-Muster des LIMIT-Datensatzes fehlerfrei abzubilden.
Geometrische Flaschenhälse
Warum scheitern Vektoren dort, wo einfache Keywords triumphieren? Die Antwort liegt in der linearen Algebra.
Ein Bi-Encoder berechnet die Relevanz zwischen einer Query $q$ und einem Dokument $d$ typischerweise über das Skalarprodukt (Dot Product). Geometrisch betrachtet definiert jede Query eine Hyperebene – einen geraden Schnitt durch den Vektorraum –, die alle Dokumente in "Relevant" und "Nicht Relevant" teilt.
Damit ein System fehlerfrei funktioniert, müssen die Dokumenten-Vektoren so angeordnet sein, dass sie für jede mögliche Query durch eine einfache, gerade Schnittfläche getrennt werden können. Wenn die Attribute der Dokumente – wie im LIMIT-Datensatz – völlig unkorreliert und zufällig kombiniert sind, explodiert die geometrische Komplexität. Es existiert schlichtweg kein niedrig-dimensionaler Raum (z.B. 1024 Dimensionen), in dem man Punkte so anordnen kann, dass tausende sich widersprechende Trennungen gleichzeitig linear realisierbar sind.
Eine Frage der Kapazität: Vektoren als Container
Bedeutet dies das Ende für Vektoreinbettungen? Ist der Hype um semantische Suche eine Fata Morgana?
Wir bei Ontolux sagen: Nein. Das Ergebnis ist erwartbar, wenn wir unsere Perspektive wechseln – weg von der "Magie" des Sprachverstehens hin zur nüchternen Informationstheorie und Kompression.
Betrachten wir einen Embedding-Vektor technisch: Er ist ein Array, beispielsweise bestehend aus 1024 Fließkommazahlen (Floats).
Diese Zahlen haben eine begrenzte Präzision (oft quantisiert auf 8-Bit). Das bedeutet, wir haben eine harte, physikalische Obergrenze für die Informationsmenge, die in einem solchen Vektor gespeichert werden kann. Der Vektor ist ein Container mit fixem Fassungsvermögen.
Das Paradoxe ist: Warum "passen" lange, komplexe Wikipedia-Artikel in diesen Container, aber die kurzen, simplen Listen von Olinda Posso nicht?

Entropie und die Kunst der Vorhersage
In der Informationstheorie wird der Informationsgehalt einer Nachricht über die Entropie definiert. Vereinfacht gesagt: Wie überraschend ist eine Nachricht? Wie viele Vorhersagen können wir treffen, bevor wir die Daten gesehen haben?
Hier hilft die Analogie zur Bildkompression (z.B. JPEG), um das Problem der Vektormodelle zu visualisieren.
Stellen wir uns vor, wir müssten ein digitales Bild speichern. Ist das Bild komplett schwarz, ist die Aufgabe trivial. Da alle Pixel denselben Farbwert haben, speichert der Algorithmus lediglich "Alles ist schwarz".
Unsere Kompressionsalgorithmen funktionieren deshalb so gut, weil die meisten Bilder (und Texte) bestimmten statistischen Gesetzmäßigkeiten folgen. Ein Foto von Wolken hat Flächen und Verläufe; ein Pixel lässt Rückschlüsse auf seinen Nachbarn zu.
Betrachten wir dazu die folgende Grafik:
Semantisches Rauschen: Warum LIMIT das Modell sprengt
Wenn wir diese Analogie auf das LIMIT-Paper übertragen, wird das Dilemma der Vektormodelle offensichtlich: Ein Vektor mit einer Dimension von 1024 ist wie eine komprimierte JPEG-Datei mit fester Dateigröße.
- Ein typischer Wikipedia-Artikel verhält sich wie das Wimmelbild. Die Informationen sind stark korreliert. Wenn der Text von "Grasland" spricht, ist das Auftauchen von Wörtern wie "Bison" oder "Wind" statistisch sehr wahrscheinlich. Das Modell (der Encoder) nutzt sein internalisiertes "Weltwissen", um die Essenz des Artikels effizient in den Vektor zu komprimieren.
- Die LIMIT-Dokumente verhalten sich wie das statische Rauschen. "Olinda Posso" mag "Die Industrielle Revolution" UND "Ratten" UND "Gerätetauchen". Es gibt keinen kausalen Zusammenhang. Für das Modell ist dies semantisches Rauschen.
Um dieses Dokument suchbar zu machen, kann sich das Modell nicht auf Weltwissen stützen ("Wer Ratten mag, mag oft auch Haustiere"). Es muss versuchen, jede einzelne dieser unzusammenhängenden Fakten "hard-coded" in die begrenzten Fließkommazahlen des Vektors zu quetschen. Das Paper zeigt mathematisch: Die "Bandbreite" (Kanalkapazität) eines einzelnen Vektors reicht schlicht nicht aus, um diese hohe Entropie so abzubilden, dass sie abgrenzbar bleibt.
Fazit: Das Plädoyer für Hybride Systeme
Bedeutet dies nun, dass Vektordatenbanken nutzlos sind? Keineswegs. Das Paper bestätigt vielmehr eine Weisheit, die in der Information-Retrieval-Community (und in unserer Arbeit bei Ontolux) schon lange bekannt ist: No Free Lunch.
- Dense Retrieval (Embeddings): Fantastische "semantische Kompressoren". Sie glänzen bei unscharfen Zusammenhängen, Synonymen und kontextuellem Verständnis.
- Sparse Retrieval (BM25/Keyword): Die alte Garde. BM25 versucht nicht, Bedeutung zu komprimieren. Es arbeitet im extrem hochdimensionalen Raum des Vokabulars. Wenn ein Dokument das Wort "Ratten" enthält, wird dies exakt indiziert. Deshalb lösen solche Systeme den LIMIT-Task mühelos.
Das Paper von Weller et al. ist kein Abgesang auf Vektormodelle, sondern eine theoretische Fundierung für Hybride Suche.
Wer heute robuste RAG-Systeme und KI-Suche baut, darf sich nicht allein auf die "Magie" der Embeddings verlassen. Die Kombination aus der semantischen Breite von Vektormodellen (für die Absicht) und der präzisen Indexierung von Keywords (für harte Fakten) ist der einzige Weg, um die Grenzen der Informationstheorie zu respektieren.
Wir lernen: Vektoren haben eine Kapazitätsgrenze. Und manchmal ist ein einfaches Keyword der beste Weg, um im Rauschen die Nadel im Heuhaufen zu finden.
Datum: 25.11.2025
Bildquelle: Korrelationsplot aus „Which Humans?“ (Atari et al., 2023)
In unserer monatlichen Serie “KI-Journal Club” stellen wir wissenschaftliche Beiträge und Presseberichte vor aus den Bereichen Text Mining, Machine Learning, Generative Künstlicher Intelligenz & Natural Language Processing.
Wir beraten Sie gerne.
Sprechen Sie uns an

Bertram Sändig
Bertram ist Experte für KI- und Machine-Learning-Systeme mit einem Fokus auf NLP und Neural Search. Er hält einen B.Sc. in Informatik der FH Brandenburg und seit 2018 einen M.Sc. der TU Berlin mti den Schwerpunkten Machine Learning und Robotik. Parallel zum Studium war er fünf Jahre Leitender Software-Ingenieur im Space Rover Project des Luft- und Raumfahrtsinstituts der TU-Berlin. 2018 stieg er als Machine Learning Engineer bei Neofonie ein und leitet heute das Machine Learning Team bei ontolux, einer Marke der Neofonie GmbH. Mit großer Leidenschaft überführt er aktuelle Forschungsergebnisse in nutzbare Anwendungen für Kunden, vor allem an der Anpassung, Optimierung und Integration von Large Language Modellen in Suchsysteme und das Textanalyse-Toolkit von ontolux.
